Universal Law of Gravitation

Two point masses of mass $4m$ and $m$, respectively, separated by distance $d$ are revolving under mutual force of attraction. The ratio of their kinetic energies will be

A mass is at the centre of a square, with four masses at the corners as shown: 

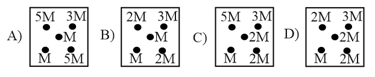
Rank the choice according to the magnitude of the gravitational force of the center mass. 

A satellite is launched in the equatorial plane in such a way that it can transmit signals up to $60°$ latitude on the earth. The angular velocity of the satellite is $\sqrt{\frac{GM}{n{R}^3}}$. Find $n$.

 The gravitational field on earth is the_____${\text{N kg}}^{-1}$.

Two masses,$800kg and 450kg$ are at a distance $25m$ apart.The magnitude of gravitational field intensity at a point $20m$ distant from the $800kg$ mass and $15m$ distant from the $450kg$ mass is $\sqrt{x}G$ (in $N/kg$).Then $x$ is-

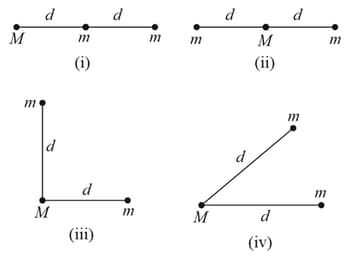
Three particles, two with masses $m$ and one with mass$M$, might be arranged in any of the four configurations shown below. Rank the configurations according to the magnitude of the gravitational force on $M$ least to greatest

The ratio of mean distances of three planets from the sun are $0.5:1:1.5$ then the square of time periods are in the ratio of

Satellite is revolving around the earth. If its radius of orbit is increased to $4$ times of the radius of geostationary satellite, what will become its time period?

The gravitational force between two objects is $F$. If masses of both the objects are halved without altering the distance between them, then the gravitational force would become

A satellite is orbiting a planet in a circular orbit of radius $1\times {10}^7 \mathrm{m}.$ The gravitational force $F$ on the satellite due to the planet is $80 \mathrm{N}.$ What would be the new $F$ if the orbit radius is doubled to $2\times {10}^7 \mathrm{m}?$

A planet of density $\rho$ is rotating with time period $T$ about its own axis. Find the smallest possible time of rotation of the planet, such that a particle is remaining in contact with the planet on the equator.
$\left(\frac{3\pi }{\rho G}=4\times {10}^6 \mathrm{S}.\mathrm{I}.\mathrm{units}\right)$

Calculate the force of attraction between a spherical shell of mass $20 \mathrm{kg}$ and radius $2 \mathrm{m}$ and a point mass $5 \mathrm{kg}$ which is at a distance of $1 \mathrm{m}$ from the center of the spherical shell.

The force of attraction due to a hollow spherical shell of uniform density, on a point mass situated inside it is _____.

The force of attraction due to a hollow spherical shell of uniform density on a point mass situated inside it is zero.

What is the force of attraction between a hollow spherical shell of uniform density and a point mass located inside the shell?

What is the magnitude of force acting between a hollow sphere of mass $M$, radius $R$ and an object of mass $m$ lying outside the sphere at a distance of $r$ from the center of the sphere?

What is the direction of gravitational force between a hollow spherical shell of uniform density and a point mass situated outside the shell?

The force of attraction between a hollow spherical shell of uniform density and a point mass situated outside is just as if the entire mass of the shell is concentrated at the _____ of the shell.

The force of attraction due to a hollow spherical shell of uniform density on a point mass situated outside is zero.

Write a short note on the force of attraction between a hollow spherical shell of uniform density and a point mass situated outside.